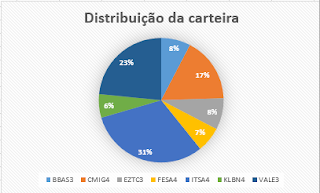
Eu gostaria de te propor uma reflexão, caro leitor. Vamos supor que eu tenha uma folha de papel, cuja espessura seja de 1 milímetro. Se eu dobrar essa folha ao meio, o resultado seria uma folha dobrada com espessura total de 2 milímetros, certo? E, se eu dobrasse novamente, teríamos uma folha dobrada com espessura de 4 milímetros, e assim por diante.
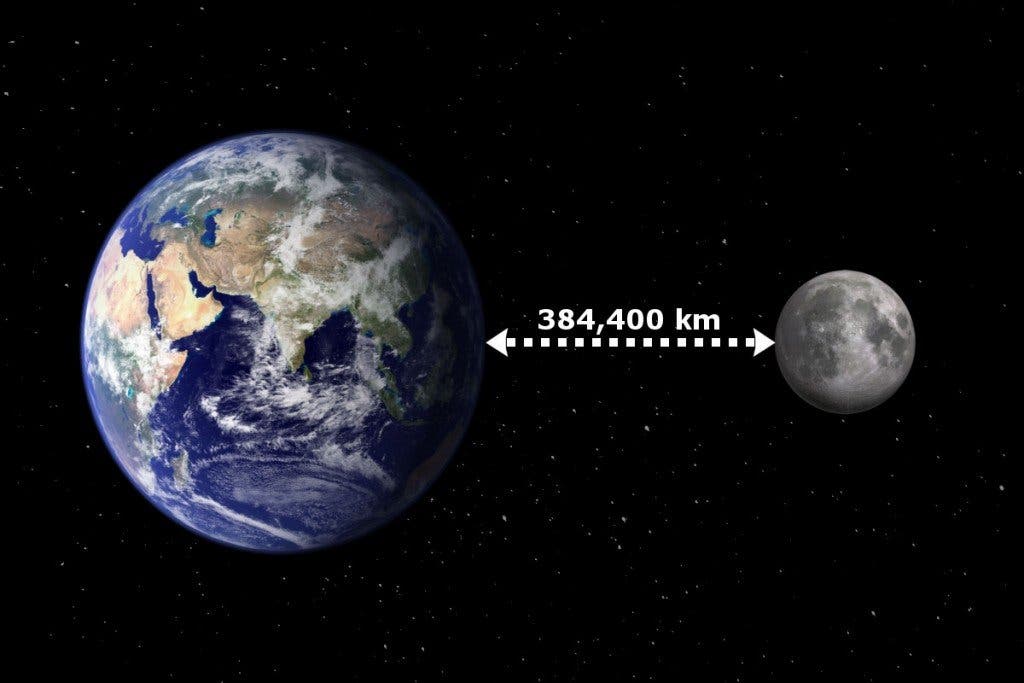
Agora imagine que não haja limitações físicas para que eu dobre essa folha indefinidamente, quantas vezes eu quiser. Quantas vezes você acha que seria necessário dobrar essa folha para que a espessura total fosse equivalente à distância da Terra à Lua?
"Já sei, estoico! Você vai tentar me pegar. Eu vou ficar aqui pensando um número bem grande, algo em torno de um bilhão de vezes, e então você vai me surpreender com um número bem menor - algo como mil vezes, certo?". Se você pensou assim ou coisa parecida, você errou feio! Bastaria que eu dobrasse o papel míseras 39 vezes para que a espessura total fosse equivalente à distância da Terra à Lua!!! (Maior, inclusive!)
Não acredita? Pois bem, eu provo. Se você dobrar o papel uma vez, a espessura total será de 1,0 mm vezes 2, que dá 2,0 mm. Se você dobra duas vezes, a espessura será de 1,0 mm vezes (2)^2 (dois elevado a dois), que dá 1,0 mm vezes 4 = 4,0 mm. Observe que a cada vez que você dobra o papel, você multiplica a espessura anterior por 2. Se você dobra a terceira vez, teremos o número da vez anterior multiplicado por 2 (pois você está dobrando), ou seja, 1,0 mm vezes ((2)^2)^2, ou 1,0 mm vezes (2)^3 (dois elevado a 3), que dá 8,0 mm.
De uma forma geral, se dobrarmos N vezes um papel com espessura de 1,0 mm teremos uma espessura total de 1,0 mm vezes 2 elevado a N, ou seja, 1,0 mm vezes 2^N. Se o papel for dobrado 39 vezes, teremos a espessura de 1,0 mm vezes 2^39. Isso dá exatamente uma espessura de 549755,813888 km! E a distância da Terra à Lua é de incríveis 384400 km!
Ficou impressionado(a)? Provavelmente sim. Eu também fiquei. E isso porque trata-se de uma função exponencial. O astrofísico Carl Sagan, em um dos seus livros, afirmou que a função exponencial não é algo intuitivo para o ser humano. Nós estamos acostumados a pensar nas coisas que crescem linearmente - se eu tenho x num determinado período, terei 2x no dobro desse tempo, e 3x no triplo desse tempo. A exponencial não é assim. Ela começa a crescer bem devagar (de 1 mm, para 2 mm, depois 4 mm, depois 8, e assim por diante) e, de uma hora para outra, explode em números assustadores!
E o que tem a ver esse papo todo de exponencial? Tem a ver que quando investimos no longo prazo, o montante cresce no forma exponencial. Tanto na renda fixa, com os juros compostos, quanto na renda variável, se você investir em bons ativos e reinvestir os lucros. Acredite em mim - se você se propor a construir patrimônio ao longo da vida, é provável que você se sinta desanimado no começo, porque verá que seu montante ainda é pequeno, e os rendimentos serão pífios. Mas, se você tiver paciência e disciplina, acredite em mim, verá seu patrimônio crescer de forma assustadora. Quer um exemplo disso?
Leia o meu post sobre a Itausa.
Prometo nos próximos posts trazer mais exemplos para te convencer que o investimento a longo prazo é imbatível. Por hoje é só.
Sejamos bons para que sejamos livres!